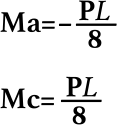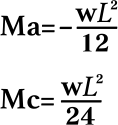みなさん、こんにちは。基礎用語、案内役のあるるです。
今回注目する基礎用語は、コチラ！
↓↓↓
今月の基礎用語：シ　＃046
ジョイントブラケット

（joint bracket）

あるる「おっ、ラーメンができましたよ！」

博士「久しぶりの富山ラーメン、うまそうじゃのぅ。あるるよ、誘ってくれてありがとう」

あるる「はいっ！　近所に新しく富山ラーメン専門店ができたので、最初に行くなら博士と、って決めてました」

博士「良い子じゃ、良い子じゃ。よし、食べようぞ」

あるる「はいっ！！（ずるずる〜〜〜）」

博士・あるる「ん、うまいっ！！」

あるる「あれ？　そういえば、二人並んでラーメンを食べるって、なんだか懐かしいような・・・」

博士「そうじゃったかの？」

あるる「ほら、博士ぇ〜、覚えてませんか？　ラーメン食べながら『ラーメン』の話、したじゃないですか？」

博士「おお、そうじゃった。ラーメンといえば・・せーの」

あるる「ラーメン小僧！」

博士「ラーメン構造じゃ（笑）　あるるよ、ラーメン小僧は覚えていても、ラーメン構造の説明はちゃんとできるのかの？」

あるる「・・・（ずるずるずる〜〜〜）」

博士「よし、このラーメンを食べ終わったら、午後からラーメン構造の復習じゃ。今度こそ、ちゃんと覚えるのじゃそ、ラーメン小僧さん」

あるる「・・・はい・・・（ずるずるずる〜〜〜）」

ラーメン大好きラーメン小僧

出来上がったものを改造・延長する場合や、定尺長さを越えるものが必要な場合において、アルミフレームを軸方向につなぎたい場合があります。

まず強度を必要とせず、出っ張りを嫌う場合には、長ナット（NSLシリーズ）を使用するのが手軽です。

セットスクリューで固定することで、外形を変えずに延長が可能です。

長ナット（NSLシリーズ）

もう少し強度が必要で外形の出っ張りが許されれば、

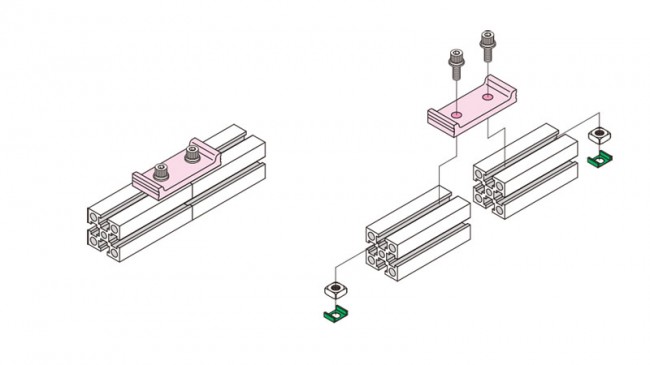
プレートブラケット（ABSPシリーズ）や

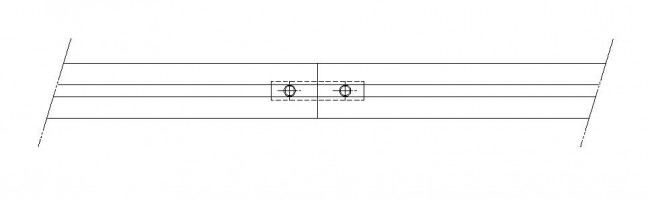
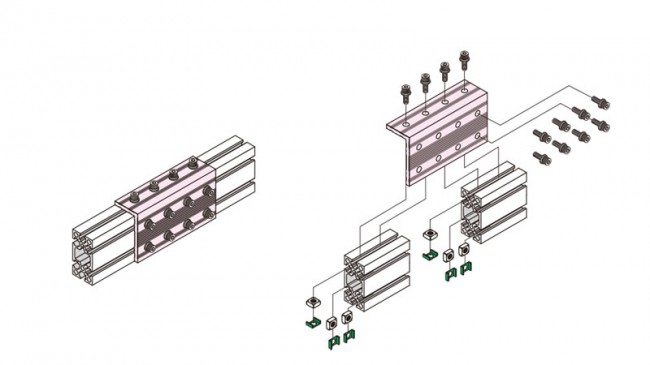
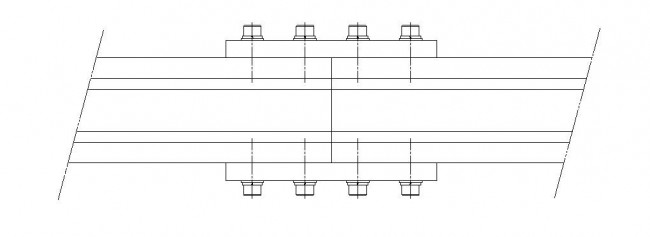
ジョイントブラケット（ABJL-60120-6）を使用するのが良いです。

プレートブラケット（ABSPシリーズ）

ジョイントブラケット（ABJL-60120-6）

慎重に考える必要があるのは、荷重のかかる長い梁です。

大きなブースの天井などで定尺では長さが足りない場合、ラーメン構造として上下別のエリアで接続することが無難な方法です。

しかし、本来長いフレームが存在すれば強度的に問題ないのなら、しっかりつなぐ方法があればよいわけです。

ここは『今月のまめ知識　第29回　応力とは』で、両端固定はり中央集中荷重の場合は、端から1/4の位置で曲げモーメントが「0」になるという話をしました。

ここを掘り下げると、曲げモーメントは「0」ですが、せん断応力はあります。

また、等分布荷重では様子が異なってきます。

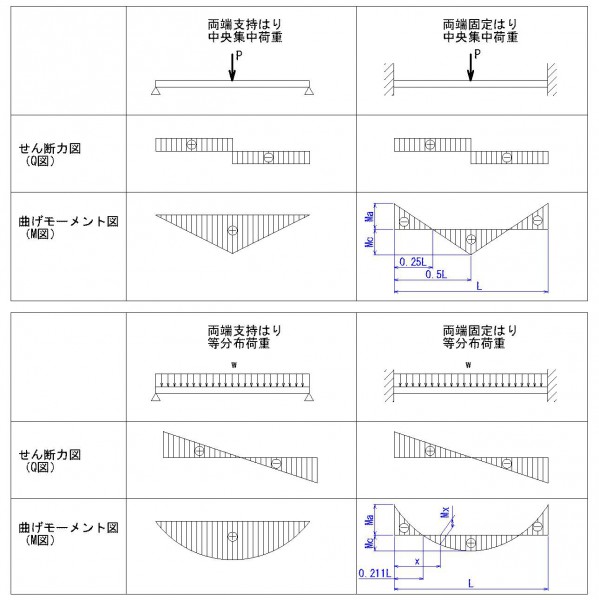
以下に、各条件でのせん断力図と曲げモーメント図を示します。

せん断力図と曲げモーメント図

通常、両端を強固に結合するとして、両端固定はりで考えます。

特に積載物のない天井梁であれば等分布荷重となりますし、中央部にFFUなど積載されれば集中荷重も加わることになります。

等分布荷重では端から21.1%の位置、集中荷重では25%の位置で曲げモーメントが「0」になります。

つまり、通常の梁ではこの21.1%から25%の間に曲げモーメントが「0」になる位置があるわけです。

この位置より内側では、はりの上側に圧縮、下側に引張りが掛かっており、外側では上側に引張り、下側に圧縮が掛かっています。

ですからこの近辺でつなげば、曲げモーメントが小さい→接合部が開こうとしないわけです。

ただし、せん断力はかかりますから、それに対応できる接続をすれば良いわけです。

せん断力を計算して、それに応じたフラットバーを上下に当てれば良いでしょう。

簡易的にはこのフラットバーが母材と同材質であった場合、上下のフラットバーの断面積が母材アルミフレームの断面積以上であれば問題ありません。

また、ボルト座面のせん断面積もこのせん断力に耐える必要があるのでここも注意が必要です。

両端固定はり中央集中荷重において

であり、曲げモーメント線図は直線なので、曲げモーメントが「0」となる位置は0.25Lとなる。

Maは上側が引張りなので符号はマイナス、

Mcは上側が圧縮なので符号はプラスになります。

両端固定はり等分布荷重において

であり、絶対値としてはMaはMcの2倍になる。

ｘの位置での曲げモーメントは

Mx＝(w/2)(Lx-x2)-wL2/12＝-wL2/2(x2/L2-x/L+1/6)

Mxを「0」とするためには

0＝x2/L2-x/L+1/6

となり、x/L＝zとすると

0＝z2-z+1/6

＝6z2-6z+1

ここで、通常の2次方程式として解くと

z=0.21133、0.78866　の２種類の解が求まり、

曲げモーメントが「0」となる位置は、端より21.1%の位置となります。

博士「どうじゃ、ラーメン小僧さんよ、わかったかの？」

あるる「ラーメンは大好きですが、その呼び方、やめてもらえますか？　“あるる”というれっきとした名前があるのですから」

博士「ふぉっふぉっふぉっ、それは失礼。でも、とっても似合っておるぞ」

あるる「それにしても、アルミフレームのつなぎ方って奥が深いですね〜。ポイントは『せん断力』と『曲げモーメント』ですね」

博士「その通り！　そこがわかっていれば大したもんじゃ。では明日あたりテストをするかのぅ。結果が楽しみじゃ」

あるる「明日、テスト？！　ジャストモーメント〜〜〜。明日は早すぎます。せめて来週に・・・」

博士「（にやにや）」